Study Results
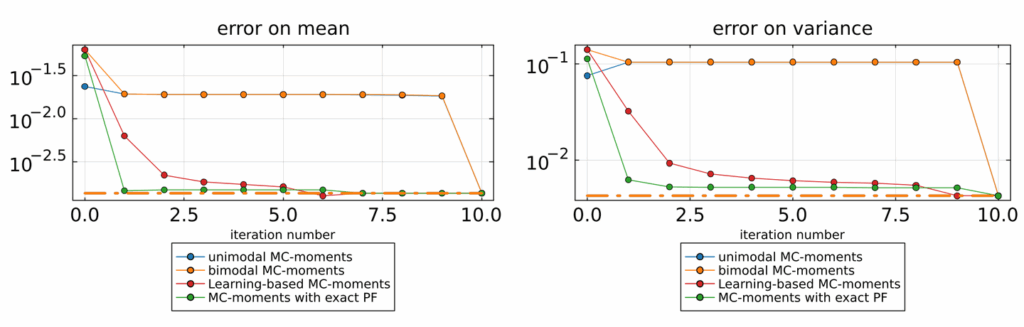
The project focused on algorithm design and analysis for high-dimensional multiscale partial differential equations that are simulated with a Monte Carlo method. We aimed to alleviate the serial bottleneck of PinT methods by considering approximate, low-dimensional models during the serial step. This led to the MC-moments Parareal algorithm for the simulation of McKean-Vlasov equations, where a coarse only simulates the first two statistical moments of the underlying SDE.
Moreover, we designed PinT methods for uncertainty quantification and data assimilation, which in themselves already require an iterative procedure. By combining those iterations, we significantly reduced computational overhead (the MLMC+Parareal algorithm). One benchmark study showed a reduction of the overall time bottleneck by 57.7% compared to the multilevel Monte-Carlo reference solution due to time parallelisation. Because of the iterative nature of the time- parallelisation, total computational effort increased with 1.1% compared to multilevel Monte Carlo. The combined method brings the overall computational work to 8.3% of the standard Monte-Carlo method while being significantly faster in wall-clock time.
The code for this study is written in the Julia programming language (https://julialang.org/), a high- performance dynamic programming language for scientific computing. The MultilevelEstimators.jl package (https://github.com/PieterjanRobbe/MultilevelEstimators.jl) implements – among others – a Multi-Level Monte Carlo method. A fork of this code with some compatibility modifications was used within the study, see (https://github.com/Rbthn/MultilevelEstimators.jl). The Parareal algorithm implementation used for the study relies on the Distributed computing framework within the Julia language. The implementation can be found at (https://github.com/Rbthn/parareal). The code tying it all together, as well as scripts and models is located at (https://github.com/Rbthn/mlmc-parareal).
Benefits
With exascale computing, we have the potential to dramatically improve our capabilities in simulation and prediction, virtual experimentation, rapid prototyping and real-time control. This will create a huge number of new possibilities for existing and new companies and for new market opportunities. With the development of PinT methods, to which this project contributes, we will be able to exploit exascale power in two settings:
- Time-critical applications, e.g., in weather prediction, computational medicine, or optimal control, where wall-clock times need to be low so that simulations can be integrated into an operational workflow. In applications where this is currently possible, this usually implies that uncertainty quantification is either neglected or performed purely based on sensitivity analysis.
- Extreme-scale applications, e.g., in climate modelling, fusion energy, or virtual prototyping in other application domains. The fundamental physical principles of electromagnetic simulations are encoded in parabolic and hyperbolic partial differential equations with uncertain coefficients or forcing terms. These types of mathematical models are ubiquitous in science and engineering, and hence methods developed in this project have significant application potential in other domains.
The broad range of possible applications will enable new companies, new jobs, new business models, and new simulation-based services for, e.g., medical or engineering applications. These services will hide the complexity of exascale computing from the end-user, but they will deliver immediate response for time-critical applications.
Partners
| NUMA (Numerical Analysis and Applied Mathematics) at KU Leuven develops and analyses numerical algorithms and software for large-scale problems in science and engineering. This research comprises the range from fundamental research (exploration of novel approximation strategies and numerical analysis) to software implementation and applications in other domains. |
| CEM (Computational Electromagnetics) at TU Darmstadt is embedded into the department of Electrical Engineering and Information Technology (ETIT) as well as the Center for Computational Engineering (CE) at TU Darmstadt. Its teaching and research are focused on modelling, simulation and optimization of electrotechnical systems |
Team
- Robert Hahn
- Sebastian Schöps
- Ignace Bossuyt
- Giovanni Samaey
Contact
Name: Giovanni Samaey
Institution: KU Leuven
Email Address: Giovanni.Samaey@kuleuven.be