Highlights
- Developed a 4D multilevel block decomposition for the Dirac operator within QUDA
- Applied multilevel techniques to improve statistical accuracy while reducing computational costs by leveraging locality
- Implemented multigrid methods to enhance low-mode averaging efficiency in Lattice QCD simulations
- Reduced computational overhead and statistical noise, enabling more precise hadronic physics calculations
- Optimized algorithms for scalability on exascale GPU-based architectures
- Strengthened collaboration between supercomputing centers and the Lattice QCD research community
| Keywords | High-Performance Computing, Quantum Chromodynamics, Computational Physics, Lattice QCD, Domain Decomposition, Energy, Engineering |
| Technologies used | GPU, HPC, LQCD, AMG, LMA |


Challenge
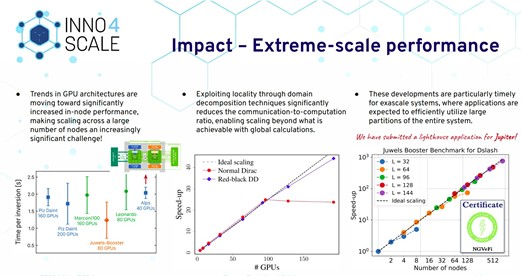
Lattice Quantum Chromodynamics (QCD) calculations are computationally intensive due to their large problem size, requiring high-resolution grids and extensive statistical ensembles. A critical step in these calculations is inverting the Dirac operator to compute quark propagators, essential for studying hadrons. However, this operator is poorly conditioned, particularly for light quark masses, making solvers computationally expensive. Standard algorithms face long convergence times and high noise levels, limiting precision. Over the past decade, multigrid solvers have mitigated critical slow-down by using multiple levels of coarsening to reduce problem size and accelerate convergence while preserving key low-mode information of the Dirac operator. However, this coarsening process also limits scalability. As computing moves toward exascale architectures with heterogeneous components, optimizing Lattice QCD algorithms for efficiency and scalability is essential. In this study, we explored the interplay between multigrid solvers and domain decomposition techniques to overcome this coarsening challenge, improving efficiency while maintaining precision.
Research Topic
Lattice QCD is a numerical approach to solving QCD, the theory of strong interactions between quarks and gluons. It discretizes spacetime into a finite grid to make complex quantum field calculations computationally manageable. Simulating QCD on supercomputers enables precise predictions of quantities such as hadron masses, decay rates, and couplings. Lattice QCD is crucial for studying non-perturbative phenomena in the low-energy regime, which is difficult to handle analytically. It provides essential input for experiments in particle and nuclear physics.
Solution
MG4ML tackled these challenges by integrating multilevel methods and novel multigrid-based algorithms within QUDA’s framework to accelerate Lattice QCD calculations on GPUs. The multilevel block decomposition isolates active regions, allowing for more frequent measurements while reducing statistical noise, leveraging locality, and preserving accuracy. Beyond implementing a flexible 4-dimensional domain decomposition, we applied multilevel techniques to the calculation of correlations between two scalar loops, demonstrating a significant reduction in errors. Additionally, we employed multigrid solvers as an efficient low-mode averaging technique, enabling more effective low-mode computations on coarse grids compared to direct eigensolvers. Both implementations enhanced computational efficiency while lowering costs and are fully compatible with GPU-based exascale architectures, ensuring scalability for future high-performance computing systems.